Solutions to many partial differential equations must satisfy certain bounds or constraints. For instance, in hydrodynamic equations, density and pressure must remain positive, while in relativistic scenarios, the fluid velocity is capped at the speed of light. Numerical methods violating these constraints may lead to incorrect results, instability, or even simulation failure. Therefore, it is crucial to develop bound-preserving numerical methods that preserve such intrinsic constraints. Exploring provably bound-preserving schemes has attracted much attention and has been actively studied in recent years. This, however, is still a challenging task, especially for systems with nonlinear constraints, due to the absence of effective theoretical tools.

Associate Professor Kailiang Wu from the Department of Mathematics and the International Center for Mathematics at the Southern University of Science and Technology (SUSTech), in collaboration with Professor Chi-Wang Shu from the Division of Applied Mathematics at Brown University, has recently made significant progress in bound-preserving numerical methods for partial differential equations.

Their research paper, entitled “Geometric Quasilinearization Framework for Analysis and Design of Bound-Preserving Schemes,” has been published in the Research Spotlight section of the renowned journal in applied mathematics, SIAM Review.

Kailiang Wu and his team have dedicated their research to high-order structure-preserving numerical methods. They have achieved significant results on bound-preserving/physical constraint-preserving numerical schemes for compressible magnetohydrodynamics (MHD) and relativistic hydrodynamics equations. Over the years of their research, they have invented an effective quasilinearization technique for handling nonlinear constraints. Utilizing this technique, they first revealed the intrinsic relation between the bound/positivity-preserving properties of numerical MHD schemes and the divergence-free condition of the magnetic field.

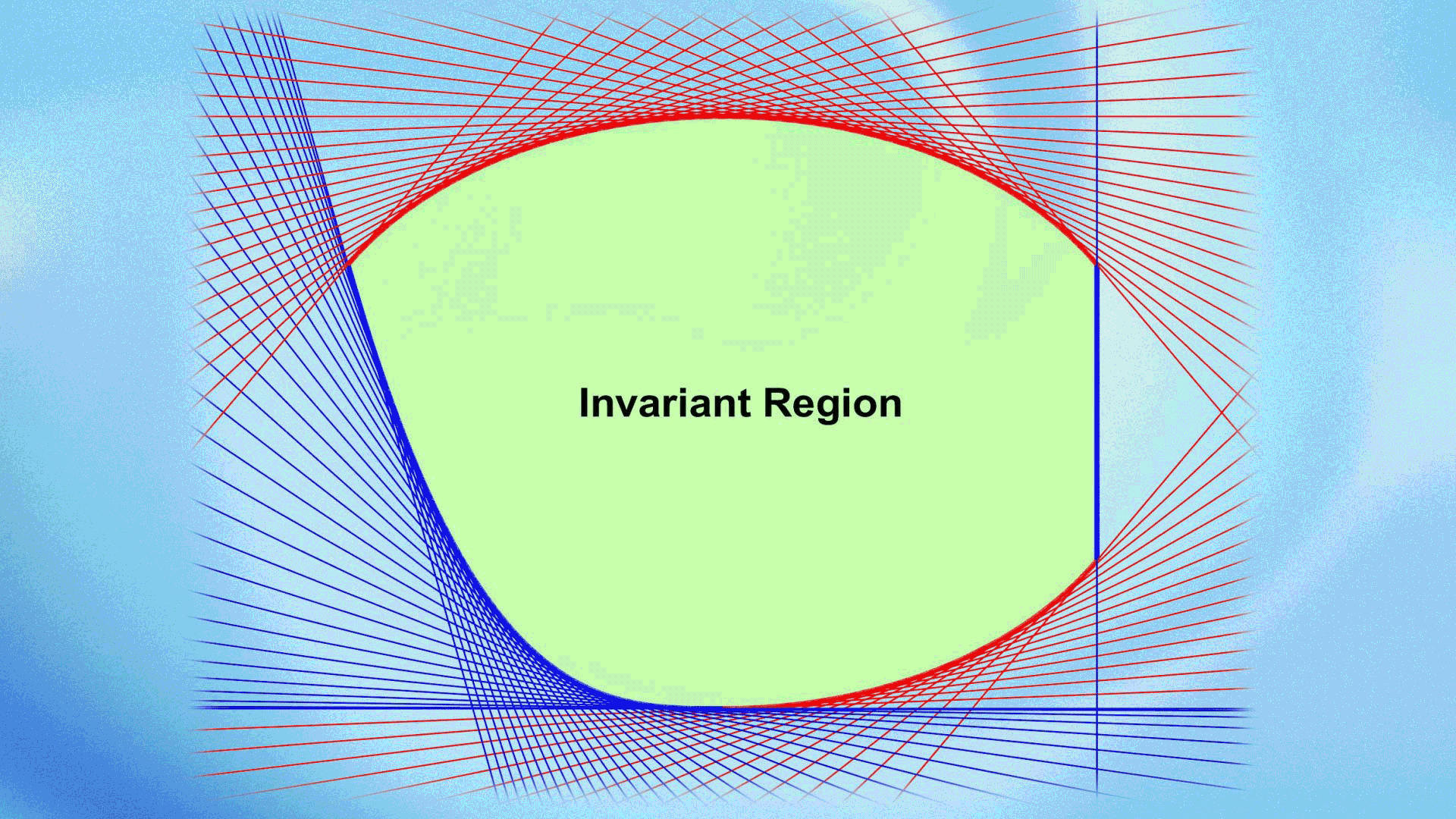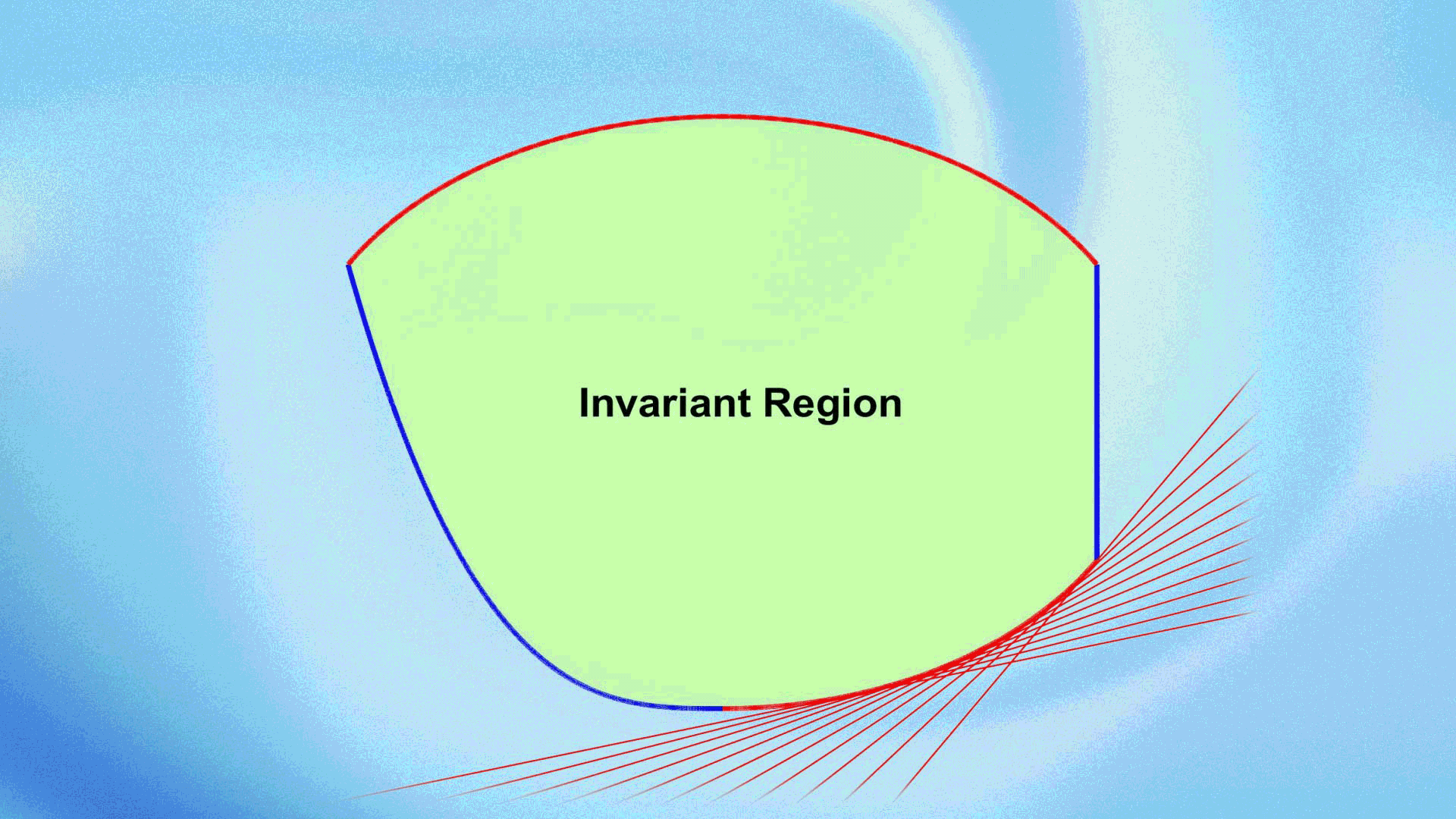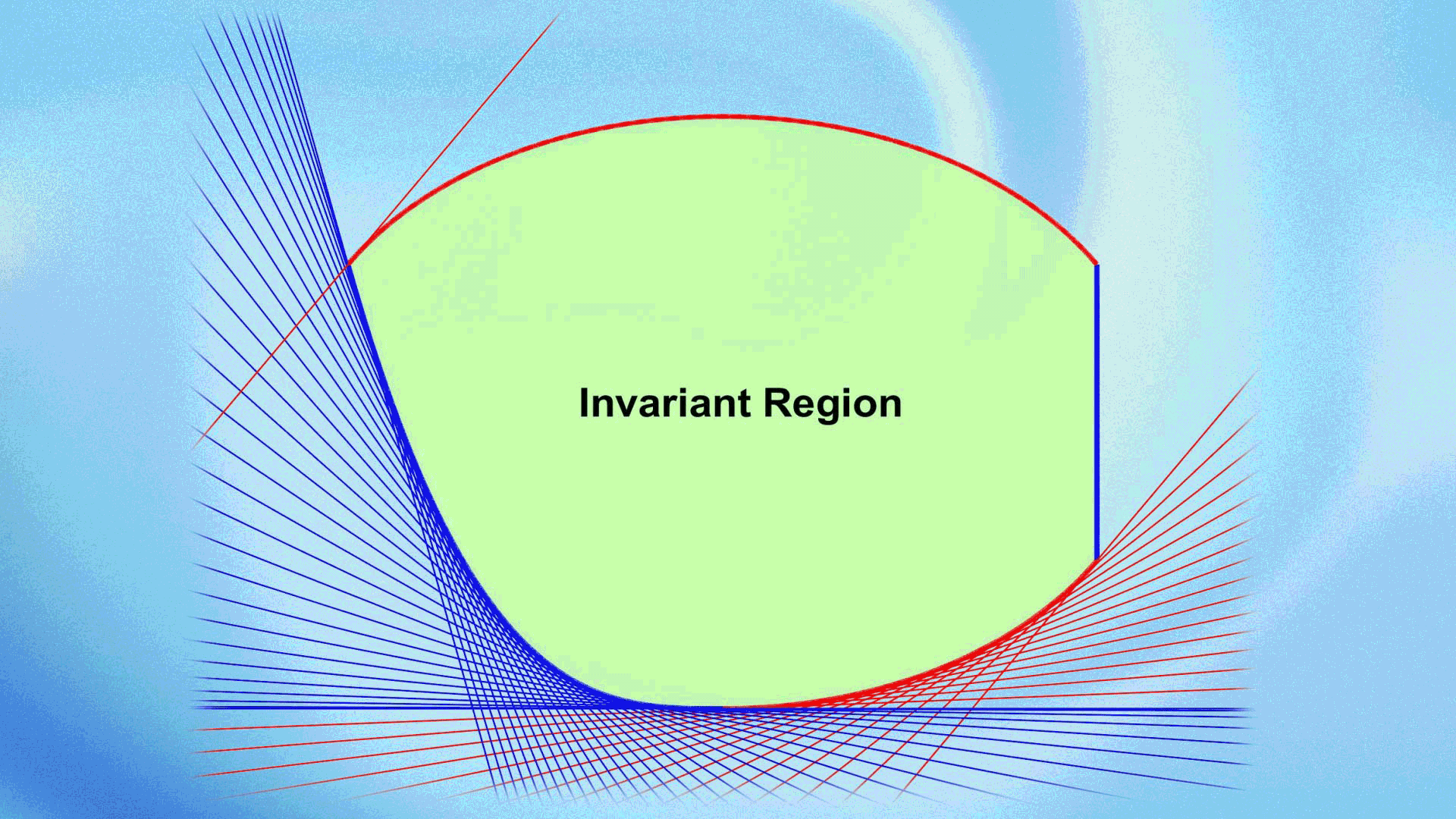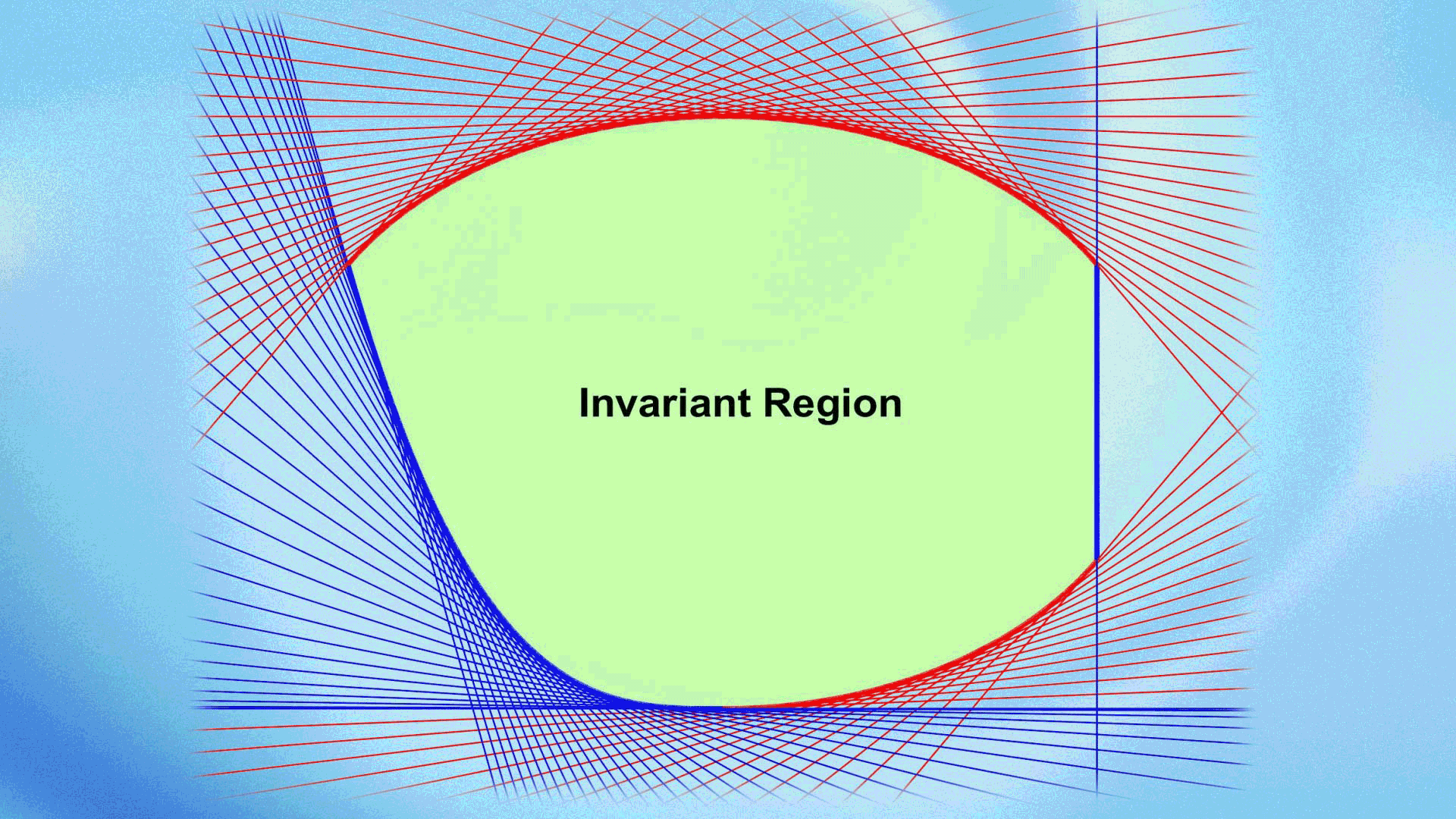
In their recent work, Kailiang Wu and Professor Chi-Wang Shu systematically proposed an innovative and general framework, termed Geometric Quasi-Linearization (GQL), inspired by key geometric insights. The GQL framework paves a new, effective way for studying bound-preserving problems with nonlinear constraints. The core idea of GQL is to equivalently transform nonlinear constraints into linear ones by introducing free auxiliary variables. By utilizing the geometric properties of convex regions, they established the fundamental principles and general theory of GQL and proposed three simple and effective methods for constructing GQL. They applied the GQL approach to various partial differential equations with nonlinear constraints, demonstrating its effectiveness and remarkable advantages. The GQL framework reveals an important mathematical principle: “nonlinear constraints that form convex sets are essentially linear when viewed from a higher dimension”.

Associate Professor Kailiang Wu is the first author of this article, and Professor Chi-Wang Shu is the corresponding author.

This research was supported in part by the National Natural Science Foundation of China (NSFC).

Paper link: https://epubs.siam.org/doi/10.1137/21M1458247