Topological order is a new quantum phase beyond Landau’s symmetry-breaking paradigm. Its defining features include robust degenerate ground states, long-range entanglement, and anyons. The characterization and measurement of topological order are not only of fundamental importance in condensed matter physics and provide the physical foundation of fault-tolerant topological quantum computers.

Anyons are particle-like topological excitations in 2D topological orders. They have fractional charges and fractional statistics. Probing anyons experimentally through transport measurement in the fractional quantum Hall effect systems has received considerable attention in recent years.

The approach of quantum simulation has also been developed to study topological orders in artificial quantum processors due to their controllability and measurability. Mathematically, the R and F matrices, which characterize the fusion-braiding properties of anyons, can uniquely identify topological order. However, it is challenging to measure these data in an experiment.

Associate Researcher Jiansheng Wu’s research group and Researcher Liang Kong at the Shenzhen Institute for Quantum Science and Engineering (SIQSE) at the Southern University of Science and Technology (SUSTech) have recently made progress in measuring fundamental physical data of topological order.

Their research paper, entitled “Uniquely identifying topological order based on boundary-bulk duality and anyon condensation,” has been published in National Science Review as a cover research article.

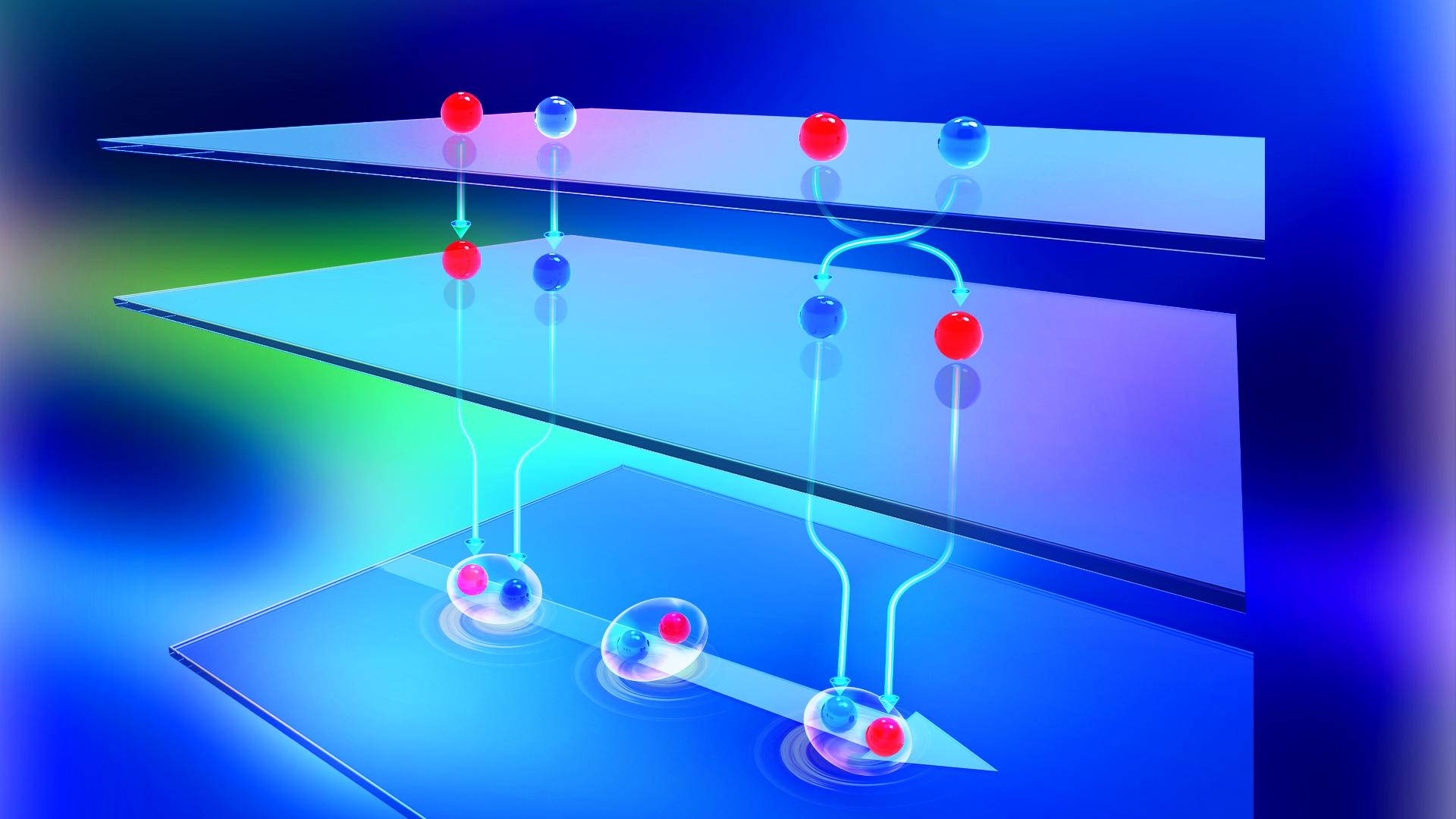
Figure 1. Cover Image

The meaning of the R and F matrices are explained as follows. Consider two processes illustrated in Figure 2(a). One is to fuse two anyons a and b to produce anyon c directly; the other is to braid (exchange) these two anyons first, then fuse them to produce anyon c. The two processes produce the same anyon c, but the final topological wavefunction differs by a transformation R-matrix. Figure 2(b) illustrates two different ways to fuse three anyons. They lead to the same final anyon, but there are different possible fusion outcomes i and j in the middle. The first set of fused states spans the same Hilbert space as the second one, and the F matrix is the transformation matrix between these two bases.

The R and F matrices are fundamental physical quantities to describe topological order. However, there has yet to be an effective measurement scheme for them. The difficulty in measuring R matrices is two-folded. First, in a lattice model, after exchanging two different anyons, apart from the difference in the topological wavefunction (the R matrix), their relative position also changed, as shown in Figure 2(c) a₇. It seems not possible to extract the R matrix directly. Second, the R matrices have different gauge equivalent forms. They are not unique and seem not to be measurable quantities.

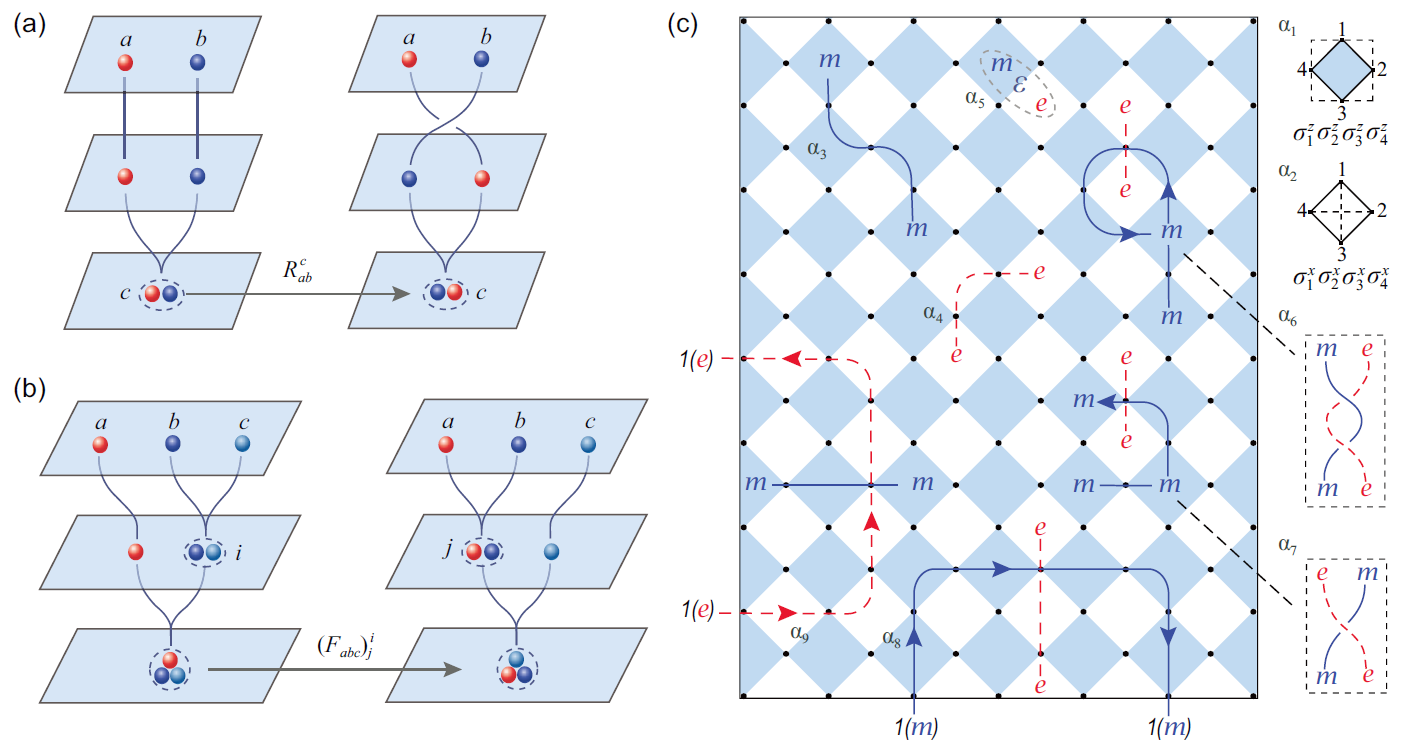
Figure 2. Graphical representations of R matrices, F matrices, and a toric code lattice with gapped boundaries

The researchers explored these problems in the toric code model. They found that the problems can be resolved through the boundary-bulk duality of topological order and anyon condensation at the boundary. If the lattice model possesses boundaries, some anyons are equivalent to the vacuum and can be created or annihilated on the boundary by local operators (they are condensed on the boundary); other anyons will remain on the boundary and become boundary excitations.

Consider creating anyons on the boundary, exchange their position with another anyon, and then annihilate the anyon on the boundary (Figure 2(c) a₈, a₉). Through this process, the anyons are exchanged. At the same time, there is no difference in the relative position of the initial and final state. Therefore, the first difficulty is solved. This process is called half-braiding. The effect of anyon exchange can be determined on the boundary by half-braiding. In other words, the bulk anyon is defined by the boundary excitation equipped with the data of half-braiding, and the boundary half-braiding defines the bulk braiding. The data of half-braiding can be directly measured in the experiment. Besides, different gauge equivalent R matrices can be obtained through half-braidings on different kinds of boundaries. Then the second difficulty is solved.

Furthermore, the data of F matrices can be measured by comparing different quantum states prepared by different orders of fusion. The researchers did a proof-of-principle demonstration on an NMR quantum processor. The non-trivial braiding of toric code m and e anyons, and an F matrix element are measured in the experiment. Therefore, the first measurement of topological order’s most fundamental physical quantities is achieved.

This work is fundamental research on the characterization and measurement of topological order. It will be enlightening in potential applications of topological order in quantum information processing.

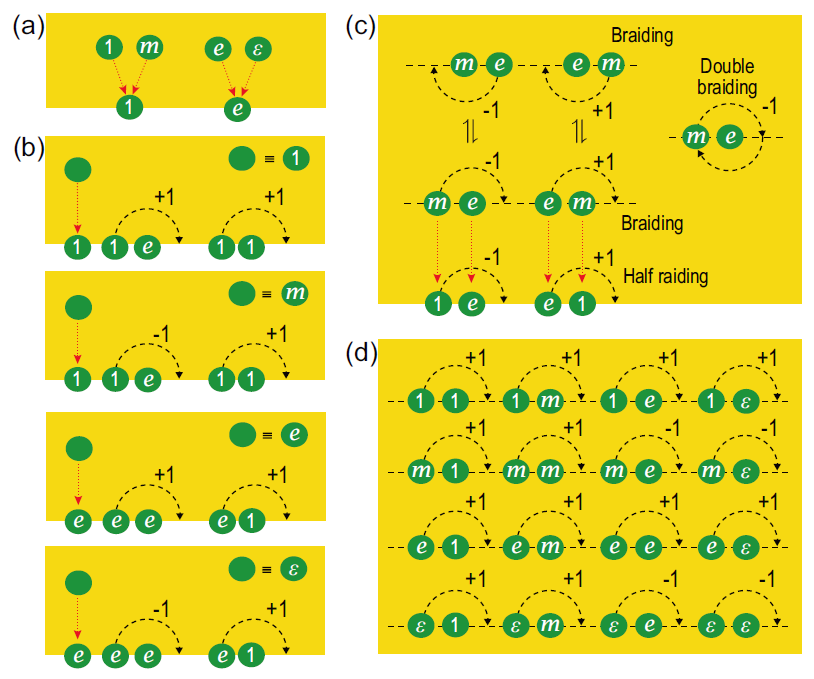
Figure 3. Anyon condensation; Define bulk anyons and their braidings by boundary excitations and their half-braidings

Yongju Hai, an undergraduate student from the Department of Physics and SIQSE at SUSTech, and Ze Zhang, a Ph.D. student from the Department of Physics, are the co-first authors of this paper. Associate Researcher Jiansheng Wu and Researcher Liang Kong from SIQSE are the corresponding authors, while other authors include Chair Professor Dapeng Yu and Hao Zheng, a former Researcher at SIQSE. SUSTech is the first affiliation of the paper.

The work was supported by the National Natural Science Foundation of China (NSFC), Department of Science and Technology of Guangdong Province, Science, Technology and Innovation Commission of Shenzhen Municipality, and SUSTech.

Paper link: https://doi.org/10.1093/nsr/nwac264