Recently, Dapeng Yu’s group (Institute for Quantum Science and Engineering, Southern University of Science and Technology) and Xiong-Jun Liu’s group (ICQM Peking University), together with Jiangong You’s group (Chern Institute of Mathematics, Nankai University) proposed a class of exactly solvable quasiperiodic mosaic models to realize mobility edges (MEs) which can be arbitrary even number in the energy spectra, depending on the parameter. They also proposed a novel scheme with high feasibility to precisely realize the model in experiment. Their study was published in a top international journal, Physical Review Letters, entitled “One-dimensional quasiperiodic mosaic lattice with exact mobility edges.”

Anderson localization is a fundamental quantum phenomenon in condensed matter physics, showing the disorder-induced localization of electronic wave-functions. The MEs in energy which separate extended and localized states are a most important concept in understanding the localization physics. If the Fermi energy is in the extended region, the system is metallic, and if the Fermi energy is in the localized region, the system is insulator. Varying the disorder strength or particle number density may shift the position of ME across Fermi energy, and induce the metal-insulator transition. Therefore, in theory and practice, the research of MEs has great significance. However, scaling theory tells us that all single-particle states are localized for arbitrarily weak random disorder strengths in one dimensional (1D) or two dimensional systems, and no MEs exist.  Therefore, for random disorder potential, MEs can exist only in dimension higher than 2. Due to the complexity of three dimensional systems, it is hard to introduce microscopic models to understand the physics of the ME in three dimensional systems. When the random disorder is replaced by quasiperiodic potential, the system may host localized and delocalized states even in the 1D regime, and so MEs may exist in 1D quasiperiodic systems. Moreover, the quasiperiodic potential can be easily realized in cold atom experiment. Therefore, quasiperiodic lattices have been widely studied in both theory and experiment.

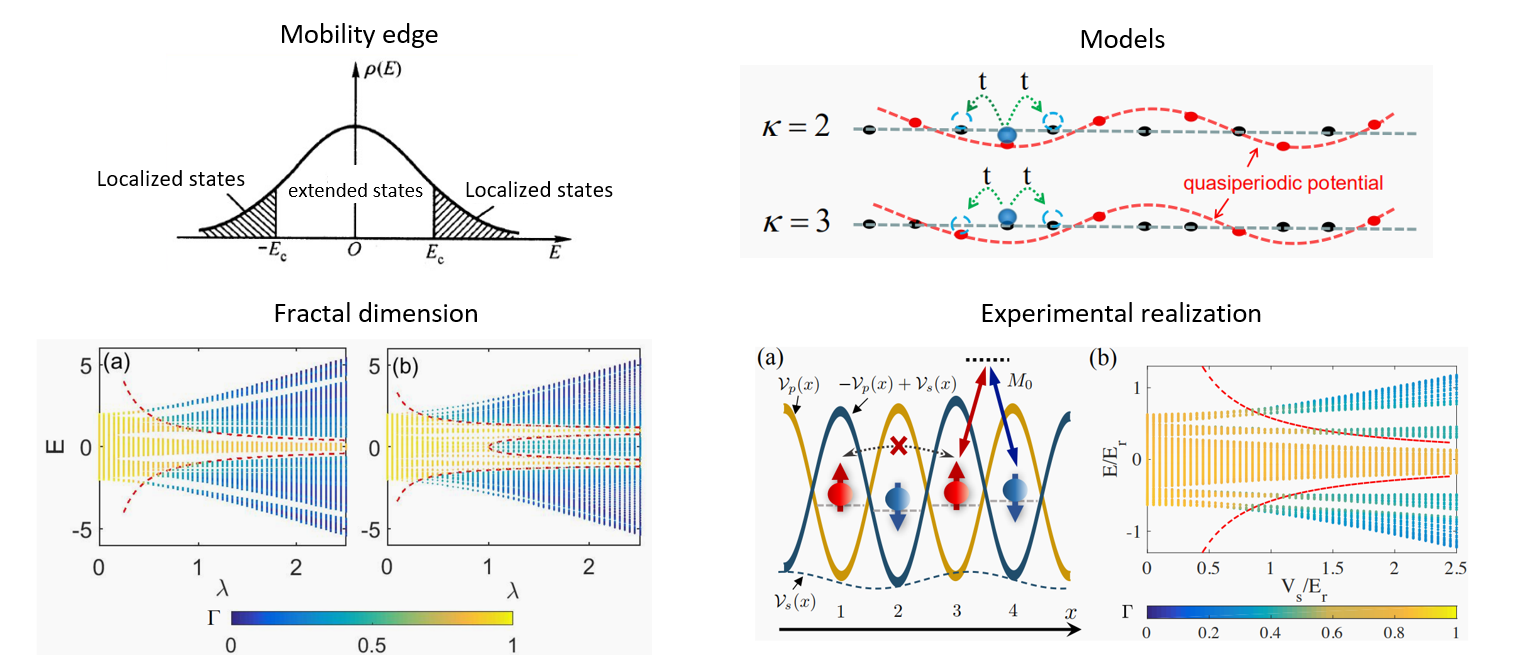
This work proposed a class of exactly solvable 1D quasiperiodic mosaic models, where quasiperiodic on-site potentials are inlaid in the lattice with equally spaced sites. Changing the integer inlay parameter of their proposed models, they can obtain arbitrary even number MEs. They applied the profound A. Avila’s global theory, one of the Fields Medal work, to these models, and provided the exact results not only for the MEs, but also for the localization and extended features of all states in the spectra.  Then they further proposed the novel scheme to realize their model based on an optical Raman lattice, which is fully within the current experimental accessibility and paves the way for experimental exploration of the predicted exact ME physics. This work provides new fundamental thoughts for the exact study of ME physics and localization physics. Since the models they proposed are elegant, exactly solvable, and experimentally realizable, the models may become the fundamental models to study ME physics.

In this work, Dr. Yucheng Wang, a postdoc at the Institute for Quantum Science and Engineering and the Department of Physics, Southern University of Science and Technology, is the first author. Dr. Xu Xia, a postdoc at Chern Institute of Mathematics, Nankai University, are the co-first author. Prof. Xiong-Jun Liu at the ICQM, Peking University and prof. Jiangong You and prof. Qi Zhou at Nankai University are the co-corresponding author.

This work was supported by the National Nature Science Foundation of China, the Science and Technology Ministry, the Department of Science and Technology of Guangdong province, Shenzhen Science and technology innovation Commission, and Southern University of Science and Technology.

Article link: https://link.aps.org/doi/10.1103/PhysRevLett.125.196604